「山読み」のアルゴリズムを評価する

牌の危険度決定アルゴリズムを評価するでは天鳳の牌譜を使って牌の危険度決定アルゴリズムの精度を評価しました。今回はいくつかの山読みアルゴリズムの候補について、同様の手法で評価してみます。

「山読み」といってもランダムに積まれている牌山を直接読むことは不可能です。打ち手の意思が入る手牌に使われている牌を推定することにより、残りの牌が牌山にあると間接的に推定することになります。つまり行うべきことは「手牌読み」という訳です。

実験方法
手牌推定アルゴリズム
評価方法
- 二乗平均平方根誤差
- 交差エントロピー誤差
評価結果

実験方法

2024年の天鳳鳳凰卓東南戦 184,426 戦について、起家目線^*1で自身のツモと副露直後のタイミング(つまり打牌直前)で毎巡相手の手牌に使われている牌を推定し、実際に使われている牌との乖離で評価します。

手牌推定アルゴリズム

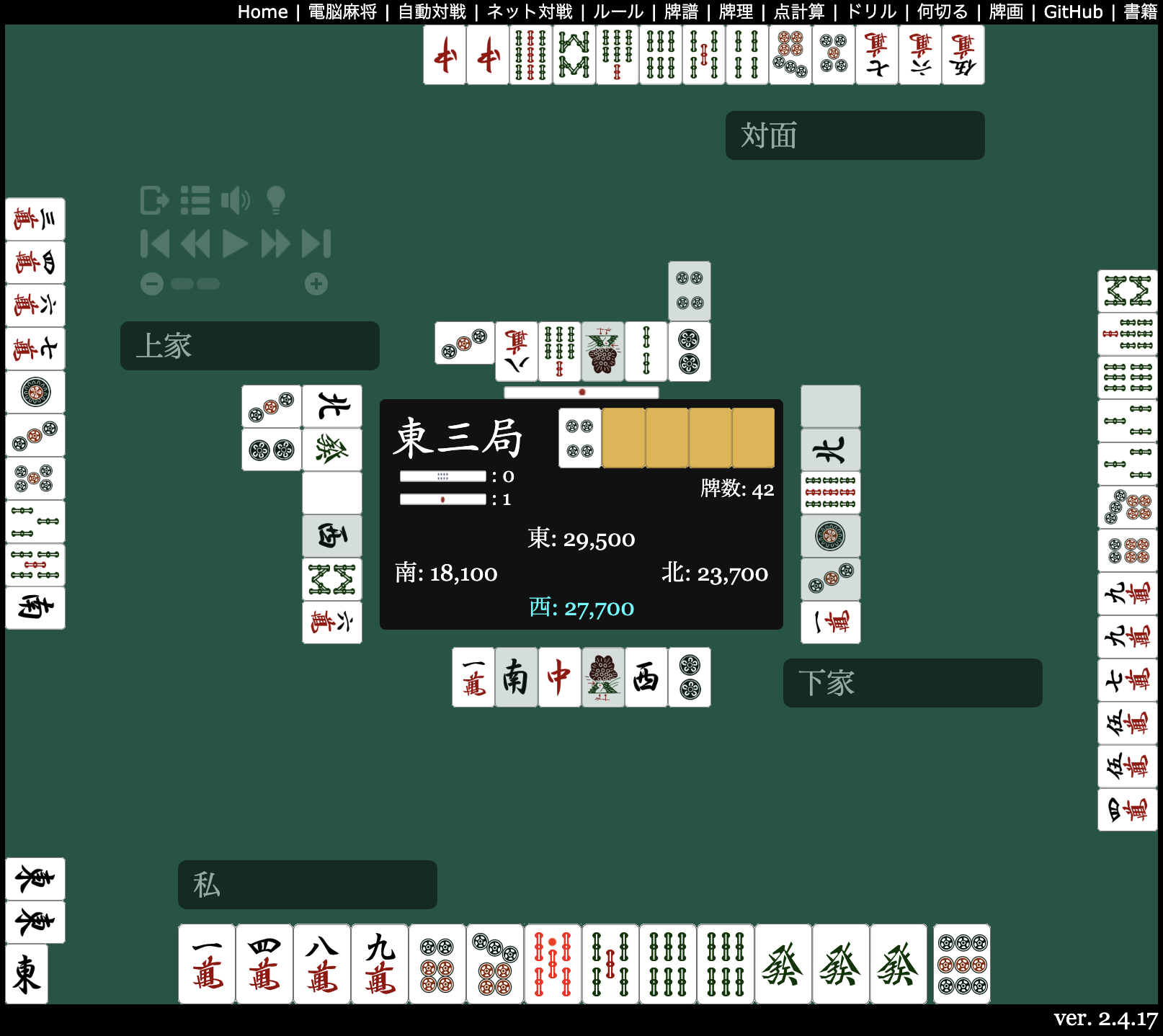
上図の局面を例に評価対象とする手牌推定アルゴリズムを説明します。推定結果は34種それぞれの牌の存在確率とし、その総和が 1 となるように正規化します(ここではこれを 手牌密度 と呼ぶことにします)。それぞれの牌について、

手牌密度 × 手牌の総数 = 手牌にあると推定される枚数

となります。

推定すべき手牌は以下の構成の36枚です。

	1	2	3	4	5	6	7	8	9
m	0	0	1	2	3	2	2	0	2
p	1	1	1	0	2	1	2	0	0
s	0	0	3	1	2	2	2	2	1
z	0	1	0	0	0	0	2

推定なし

見えていない牌の分布にしたがって、手牌と牌山に牌が存在するとします。つまり手牌密度は

見えていない枚数

に比例します。

	1	2	3	4	5	6	7	8	9
m	1	4	4	3	4	3	4	2	3
p	3	2	1	3	4	3	3	4	4
s	2	3	4	4	2	2	3	3	3
z	1	3	2	2	3	0	3

例では見えていない牌の枚数は、上記の表のとおりなので、手牌にある牌の枚数の推定は以下となります。

	1	2	3	4	5	6	7	8	9
m	0.4	1.5	1.5	1.1	1.5	1.1	1.5	0.8	1.1
p	1.1	0.8	0.4	1.1	1.5	1.1	1.1	1.5	1.5
s	0.8	1.1	1.5	1.5	0.8	0.8	1.1	1.1	1.1
z	0.4	1.1	0.8	0.8	1.1	0.0	1.1

コンボ理論

コンボ理論 ^*2 ^*3 ^*4 におけるコンボ数を使って手牌にある枚数を推定します。コンボ数とは、ある牌と雀頭あるいは面子を構成できる牌の組合せ数であり、それぞれの牌の手牌密度は

見えていない枚数 × コンボ数

に比例するとします。ただし危険度判定とは異なりスジに意味はなく、対子・刻子に使える牌は最大4枚になります^*5。

	1	2	3	4	5	6	7	8	9
m	17	26	38	50	43	42	34	27	14
p	8	9	25	24	31	42	46	31	22
s	15	30	36	34	33	26	25	21	15
z	1	6	3	3	6	0	6

例の状況でコンボ数は上記の表のとおりなので、手牌にある牌の枚数の推定は以下となります。

	1	2	3	4	5	6	7	8	9
m	0.2	1.5	2.2	2.2	2.5	1.8	2.0	0.8	0.6
p	0.4	0.3	0.4	1.1	1.8	1.8	2.0	1.8	1.3
s	0.4	1.3	2.1	2.0	1.0	0.8	1.1	0.9	0.7
z	0.0	0.3	0.1	0.1	0.3	0.0	0.3

統計的推定

天鳳統計(3) 〜局終了時の牌の分布で終局時の各牌の「居場所」の統計を取りましたが、これを利用します。必要なのは手牌にあるか河にあるかだけなので、これに限って統計を取り直しました。副露面子に関しては、鳴いた牌は河、鳴いたときに手牌から出てきた牌は手牌に分類します。この結果から各牌が手牌にある確率を下記としました。

字牌	数牌
字牌	1	2	3	4	5	6	7	8	9
0.23	0.33	0.54	0.67	0.71	0.74	0.71	0.67	0.54	0.33

それぞれの牌の手牌密度は

見えていない枚数 × 手牌にある確率

に比例するとします。

例の状況では手牌にある牌の枚数の推定は以下となります。

	1	2	3	4	5	6	7	8	9
m	0.2	1.5	1.9	1.5	2.1	1.5	1.9	0.8	0.7
p	0.7	0.8	0.5	1.5	2.1	1.5	1.4	1.5	0.9
s	0.5	1.1	1.9	2.0	1.0	1.0	1.4	1.1	0.7
z	0.2	0.5	0.3	0.3	0.5	0.0	0.5

統計コンボ

統計値とコンボ理論をともに利用し、それぞれの牌の手牌密度を

見えていない枚数 × 手牌にある確率 × コンボ数

に比例するとします。

例の状況では手牌にある牌の枚数の推定は以下となります。

	1	2	3	4	5	6	7	8	9
m	0.1	1.3	2.4	2.5	3.0	2.1	2.1	0.7	0.3
p	0.2	0.2	0.4	1.2	2.2	2.1	2.2	1.6	0.7
s	0.2	1.1	2.3	2.3	1.2	0.9	1.2	0.8	0.3
z	0.0	0.1	0.0	0.0	0.1	0.0	0.1

評価方法

牌の危険度を評価したとき同様に二乗平均平方根誤差と交差エントロピー誤差で評価します。

二乗平均平方根誤差

ある牌の推定枚数を p_i 、実際の枚数を y_i とすると、二乗平均平方根誤差は

√1/34 Σ_{i = 1〜34} ( p_i − y_i )²

で求めることができます。

例の局面におけるコンボ理論による推定の二乗平均平方根誤差は 0.89009、統計的推定では 0.82442 になります。値が 0 に近いほど推定は正しいと評価できます。

交差エントロピー誤差

実際の手牌内での牌の分布を確率変数とみなせるため、ある牌の手牌密度を p_i 、実際の確率を y_i とすると、交差エントロピー誤差は 前回とは異なり

−Σ_{i = 1〜34} y_i log( p_i )

で求めることができます。

例の局面におけるコンボ理論による推定の交差エントロピー誤差は 3.45841、統計的推定では 3.38073 です。

評価結果

2024年の天鳳鳳凰卓東南戦 1年分の牌譜データを用いて毎巡相手3名の手牌密度を計算し、それを二乗平均平方根誤差と交差エントロピー誤差で評価しました。評価には以下のプログラムを使用しました。

eval_guess_shoupai.js

評価結果は以下のとおりです。

巡目	二乗平均平方根誤差				交差エントロピー誤差
巡目	推定なし	コンボ理論	統計的推定	統計コンボ	推定なし	コンボ理論	統計的推定	統計コンボ
1	0.87131	1.02105	0.95997	1.15709	3.50270	3.66502	3.57747	3.90182
2	0.87756	0.98894	0.93523	1.11308	3.48386	3.60266	3.53038	3.80785
3	0.88152	0.96107	0.91467	1.07576	3.46306	3.54347	3.48682	3.72252
4	0.88248	0.93726	0.89729	1.04488	3.44229	3.49218	3.44890	3.65102
5	0.87996	0.91733	0.88216	1.02013	3.42211	3.45022	3.41691	3.59458
6	0.87407	0.90048	0.86811	1.00040	3.40220	3.41590	3.38936	3.55021
7	0.86537	0.88583	0.85425	0.98443	3.38184	3.38632	3.36412	3.51341
8	0.85431	0.87270	0.83994	0.97119	3.36029	3.35892	3.33939	3.48037
9	0.84119	0.86076	0.82483	0.96013	3.33700	3.33217	3.31401	3.44886
10	0.82608	0.84988	0.80871	0.95102	3.31139	3.30507	3.28718	3.41755
11	0.80881	0.84009	0.79145	0.94385	3.28317	3.27733	3.25860	3.38613
12	0.78893	0.83125	0.77259	0.93842	3.25192	3.24860	3.22783	3.35411
13	0.76611	0.82341	0.75190	0.93475	3.21729	3.21870	3.19453	3.32133
14	0.73951	0.81647	0.72891	0.93272	3.17869	3.18721	3.15824	3.28734
15	0.70852	0.81085	0.70323	0.93251	3.13589	3.15458	3.11872	3.25260
16	0.67170	0.80626	0.67410	0.93393	3.08825	3.12049	3.07547	3.21672
17	0.62754	0.80339	0.64069	0.93741	3.03571	3.08574	3.02841	3.18043
18	0.58616	0.79489	0.60899	0.93232	2.98400	3.04883	2.98121	3.14132

全体的に推定なしの誤差が一番小さいという残念な結果となりました。巡目によっては統計的推定が上回っていますが、あえて採用するほどの優位性はないと思います^*6。

牌の危険度決定アルゴリズムを評価する(2)

ダマテンの効果をシミュレーションする

TOP

^ ドラ表示牌、4者の捨て牌と副露牌、自身の手牌が把握できる状態
^ 【麻雀】コンボ理論について｜宇宙ジン VTuber
^ 【第2回】麻雀は学習で強くなるか。｜はね
^ 【コンボ理論】を学ぼう｜ハク
^ 危険度判定では1枚を視点となる対局者が持つため最大3枚だった
^ 統計的推定についてはシミュレーションしてみるかも

	1	2	3	4	5	6	7	8	9
m	0.4	1.5	1.5	1.1	1.5	1.1	1.5	0.8	1.1
p	1.1	0.8	0.4	1.1	1.5	1.1	1.1	1.5	1.5
s	0.8	1.1	1.5	1.5	0.8	0.8	1.1	1.1	1.1
z	0.4	1.1	0.8	0.8	1.1	0.0	1.1

	1	2	3	4	5	6	7	8	9
m	17	26	38	50	43	42	34	27	14
p	8	9	25	24	31	42	46	31	22
s	15	30	36	34	33	26	25	21	15
z	1	6	3	3	6	0	6

	1	2	3	4	5	6	7	8	9
m	0.2	1.5	2.2	2.2	2.5	1.8	2.0	0.8	0.6
p	0.4	0.3	0.4	1.1	1.8	1.8	2.0	1.8	1.3
s	0.4	1.3	2.1	2.0	1.0	0.8	1.1	0.9	0.7
z	0.0	0.3	0.1	0.1	0.3	0.0	0.3

	1	2	3	4	5	6	7	8	9
m	0.2	1.5	1.9	1.5	2.1	1.5	1.9	0.8	0.7
p	0.7	0.8	0.5	1.5	2.1	1.5	1.4	1.5	0.9
s	0.5	1.1	1.9	2.0	1.0	1.0	1.4	1.1	0.7
z	0.2	0.5	0.3	0.3	0.5	0.0	0.5

	1	2	3	4	5	6	7	8	9
m	0.1	1.3	2.4	2.5	3.0	2.1	2.1	0.7	0.3
p	0.2	0.2	0.4	1.2	2.2	2.1	2.2	1.6	0.7
s	0.2	1.1	2.3	2.3	1.2	0.9	1.2	0.8	0.3
z	0.0	0.1	0.0	0.0	0.1	0.0	0.1

	1	2	3	4	5	6	7	8	9
m	0.4	1.5	1.5	1.1	1.5	1.1	1.5	0.8	1.1
p	1.1	0.8	0.4	1.1	1.5	1.1	1.1	1.5	1.5
s	0.8	1.1	1.5	1.5	0.8	0.8	1.1	1.1	1.1
z	0.4	1.1	0.8	0.8	1.1	0.0	1.1

	1	2	3	4	5	6	7	8	9
m	17	26	38	50	43	42	34	27	14
p	8	9	25	24	31	42	46	31	22
s	15	30	36	34	33	26	25	21	15
z	1	6	3	3	6	0	6

	1	2	3	4	5	6	7	8	9
m	0.2	1.5	2.2	2.2	2.5	1.8	2.0	0.8	0.6
p	0.4	0.3	0.4	1.1	1.8	1.8	2.0	1.8	1.3
s	0.4	1.3	2.1	2.0	1.0	0.8	1.1	0.9	0.7
z	0.0	0.3	0.1	0.1	0.3	0.0	0.3

	1	2	3	4	5	6	7	8	9
m	0.2	1.5	1.9	1.5	2.1	1.5	1.9	0.8	0.7
p	0.7	0.8	0.5	1.5	2.1	1.5	1.4	1.5	0.9
s	0.5	1.1	1.9	2.0	1.0	1.0	1.4	1.1	0.7
z	0.2	0.5	0.3	0.3	0.5	0.0	0.5

	1	2	3	4	5	6	7	8	9
m	0.1	1.3	2.4	2.5	3.0	2.1	2.1	0.7	0.3
p	0.2	0.2	0.4	1.2	2.2	2.1	2.2	1.6	0.7
s	0.2	1.1	2.3	2.3	1.2	0.9	1.2	0.8	0.3
z	0.0	0.1	0.0	0.0	0.1	0.0	0.1

	1	2	3	4	5	6	7	8	9
m	0.4	1.5	1.5	1.1	1.5	1.1	1.5	0.8	1.1
p	1.1	0.8	0.4	1.1	1.5	1.1	1.1	1.5	1.5
s	0.8	1.1	1.5	1.5	0.8	0.8	1.1	1.1	1.1
z	0.4	1.1	0.8	0.8	1.1	0.0	1.1

	1	2	3	4	5	6	7	8	9
m	17	26	38	50	43	42	34	27	14
p	8	9	25	24	31	42	46	31	22
s	15	30	36	34	33	26	25	21	15
z	1	6	3	3	6	0	6

	1	2	3	4	5	6	7	8	9
m	0.2	1.5	2.2	2.2	2.5	1.8	2.0	0.8	0.6
p	0.4	0.3	0.4	1.1	1.8	1.8	2.0	1.8	1.3
s	0.4	1.3	2.1	2.0	1.0	0.8	1.1	0.9	0.7
z	0.0	0.3	0.1	0.1	0.3	0.0	0.3

	1	2	3	4	5	6	7	8	9
m	0.2	1.5	1.9	1.5	2.1	1.5	1.9	0.8	0.7
p	0.7	0.8	0.5	1.5	2.1	1.5	1.4	1.5	0.9
s	0.5	1.1	1.9	2.0	1.0	1.0	1.4	1.1	0.7
z	0.2	0.5	0.3	0.3	0.5	0.0	0.5

	1	2	3	4	5	6	7	8	9
m	0.1	1.3	2.4	2.5	3.0	2.1	2.1	0.7	0.3
p	0.2	0.2	0.4	1.2	2.2	2.1	2.2	1.6	0.7
s	0.2	1.1	2.3	2.3	1.2	0.9	1.2	0.8	0.3
z	0.0	0.1	0.0	0.0	0.1	0.0	0.1