麻雀の打牌選択アルゴリズム(9) 以来、8年ぶりに 電脳麻将 の打牌選択アルゴリズムを変更します。
電脳麻将では手牌の 評価値 を元に打牌を選択していますが、評価値計算 の際の「残り牌数」は「見えていない牌数」つまり、相手の手牌・牌山 に隠れている牌*1を指しています。 このため流局時でもまだ最大54枚*2が使えると判断するのですが、実際にはもう使える牌はありません。 今回「残り牌数」の総和が「ツモ可能枚数」と一致するように正規化します。 ツモ可能枚数は流局時には0枚となるため、もはや使える牌はないことが分かる訳です。
将来的には相手の手牌にある牌を推測し残りが山にあるとするいわゆる「山読み」を実装したいのですが、まずは見えていない牌の比率で山にいると仮定して残り牌数の総和がツモ可能枚数となるよう正規化します。
見えていない牌数をツモ可能枚数で正規化し、残り牌数として返す機能を追加します。 残り牌数は評価値を再帰的に計算する際に使用するので、現在の状態とは別に「先読み中」の状態として保持する必要があります。 このため、牌数カウントを担当するクラスSuanPaiとは独立した内部クラスPaishuを新たに作成します。
class Paishu {
/*
* 見えていない牌数 paishu とツモ可能枚数 n_zimo からインスタンスを生成する。
*/
constructor(paishu, n_zimo) {
this._paishu = {}; // 牌をキー、見えていない牌数を値とするハッシュ
this._sum_paishu = 0; // 見えていない牌数の総和(0 で初期化)
/* 全ての牌について枚数を paishu から _paishu に転記する。*/
for (let s of ['m','p','s','z']) {
for (let n = 0; n < paishu[s].length; n++) {
if (s == 'z' && n == 0) continue;
this._paishu[s+n] = n == 5 ? paishu[s][n] - paishu[s][0]
: paishu[s][n];
// 赤牌の枚数は赤牌以外と区別する
this._sum_paishu += this._paishu[s+n]; // 総和を加算する
}
}
this._n_zimo = n_zimo; // ツモ可能枚数
}
/*
* 牌 p のツモ可能枚数で正規化した残り牌数を返す。real が真のときは
* 正規化せず見えていない牌数をそのまま返す。
*/
val(p, real) {
return real ? this._paishu[p.slice(0,2)]
: this._n_zimo > 0 ? this._paishu[p.slice(0,2)]
* this._n_zimo / this._sum_paishu
: 0; // ツモ可能枚数がないときは 0 とする
}
/*
* 牌 p を牌山から取り出す。次のツモ巡を意味するので、ツモ可能枚数は 4 枚
* 消費する。
*/
pop(p) {
this._paishu[p.slice(0,2)]--;
this._sum_paishu--;
this._n_zimo -= 4;
return this;
}
/*
* 牌 p を牌山に返す。
*/
push(p) {
this._paishu[p.slice(0,2)]++;
this._sum_paishu++;
this._n_zimo += 4;
return this;
}
}クラスPaishuは見えていない牌数とツモ可能枚数を引数にインスタンスを生成します。 評価値計算の先読みの過程で牌を使うときにはメソッド pop()、バックトラックして牌を戻すときには push() を呼び出します。 正規化した残り牌数は val() で取得しますが、この際に見えていない枚数として取得するインタフェースも残しました。
PaishuのインスタンスはSuanPaiのメソッド get_paishu() の返り値として取得します。
/*
* 見えていない牌数 _paishu とツモ可能枚数 _n_zimo を初期化する。
*/
constructor(hongpai) {
this._paishu = {
m: [hongpai.m, 4,4,4,4,4,4,4,4,4],
p: [hongpai.p, 4,4,4,4,4,4,4,4,4],
s: [hongpai.s, 4,4,4,4,4,4,4,4,4],
z: [ 0, 4,4,4,4,4,4,4]
};
/* ...... */
this._n_zimo = 70;
}
/*
* 見えていない牌数 _paishu とツモ可能枚数 _n_zimo から Paishu の
* インスタンスを生成し、返す。
*/
get_paishu() {
return new Paishu(this._paishu, this._n_zimo);
}残り牌数の数え方が変わると評価値の値も変わります。 ツモ可能枚数は見えていない牌数より少ないので、評価値は相対的に低くなるはずです。 このため現在の評価値のスケールに合わせて調整した押し引きアルゴリズムには再調整が必要です。
再調整は今後行うとして、まず「シャンテン数とスジ・無スジ」に頼る 旧来の押し引き方法 で実装されたAI 0400 に戻し、これをベースに修正を加えます。
0400 ではSuanPaiのメソッド paishu_all() を呼び出して見えていない牌数を連想配列形式で取得していますが、これを get_paishu() に置き換え、Paishuのインスタンスを取得します。
2シャンテン以降の評価値計算では正規化した残り牌数を使用します。 3シャンテン以前は評価値計算は行わず、有効牌の多い打牌を選択していますが、このときの牌数は従来と変わらず見えていない牌数とします。
/*
* 手牌 shoupai の評価値を残り牌数 paishu を用いて計算する
* シャンテン戻しのときは back にその牌を指定する
*/
eval_shoupai(shoupai, paishu, back) {
/* ...... */
/* 評価値を計算する */
if (n_xiangting == -1) { // 和了形となっている場合
/* ...... */
}
else if (shoupai._zimo) { // 打牌可能な牌姿の場合
/* ...... */
}
else if (n_xiangting < 3) { // 打牌後の牌姿の場合(2シャンテン以降)
/* (赤牌を区別した)各々の有効牌について以下の処理を行う */
for (let p of add_hongpai(Majiang.Util.tingpai(shoupai))) {
if (p == back) { rv = 0; break } // フリテンの場合は評価値を0とする
if (paishu.val(p) == 0) continue; // 4枚切れの牌は処理しない
let new_shoupai = shoupai.clone().zimo(p);
// 手牌を複製し、牌をツモる
paishu.pop(p); // 牌 p を牌山から取り出す
let ev = this.eval_shoupai(new_shoupai, paishu, back);
// ツモ後の牌姿の評価値を求める
if (! back) { // シャンテン戻しでない場合
if (n_xiangting > 0) // テンパイしていない場合
ev += this.eval_fulou(shoupai, p, paishu, back);
// 副露後の牌姿の評価値を加える
}
paishu.push(p); // 牌 p を牌山に返す
rv += ev * paishu.val(p); // 評価値 × 牌数 の総和をとる
}
rv /= width[n_xiangting]; // シャンテン数に応じて補正する
}
else { // 3シャンテン以前の場合
for (let p of add_hongpai(this.tingpai(shoupai))) {
// (赤牌を区別した)各々の有効牌に
// ついて以下の処理を行う
if (paishu.val(p, 1) == 0) continue;
// 4枚切れの牌は処理しない
/* 牌 p の枚数(見えていない枚数)を評価値とする */
rv += paishu.val(p, 1) * ( p[2] == '+' ? 4 // ポンは4倍
: p[2] == '-' ? 2 // チーは2倍
: 1 );
}
}
/* ...... */
return rv; // 計算した評価値を返す
}
/*
* 手牌 shoupai のシャンテン戻しでの評価値を残り牌数 paishu を用いて計算する
* シャンテン戻しのときは back にその牌を指定する
*/
eval_backtrack(shoupai, paishu, back, min) {
/* ...... */
/* (赤牌を区別した)各々の有効牌について以下の処理を行う */
for (let p of add_hongpai(Majiang.Util.tingpai(shoupai))) {
if (p.replace(/0/,'5') == back) continue;
// 引き戻した牌は処理しない
if (paishu.val(p) == 0) continue;
// 4枚切れの牌は処理しない
let new_shoupai = shoupai.clone().zimo(p);
// 手牌を複製し、牌をツモる
paishu.pop(p); // 牌 p を牌山から取り出す
let ev = this.eval_shoupai(new_shoupai, paishu, back);
// ツモ後の牌姿の評価値を求める
paishu.push(p); // 牌 p を牌山に返す
if (ev - min > 0.0000001) rv += ev * paishu.val(p);
// min を超えた値の評価値のみ
// 評価値 × 牌数 の総和をとる
}
return rv / width[n_xiangting]; // シャンテン数に応じて補正する
}修正後のAIと 0400 を デュプリケート対局 で1,000戦対戦させました。 平均順位が 2.54 → 2.56 と下がったので打ち筋を確認します。
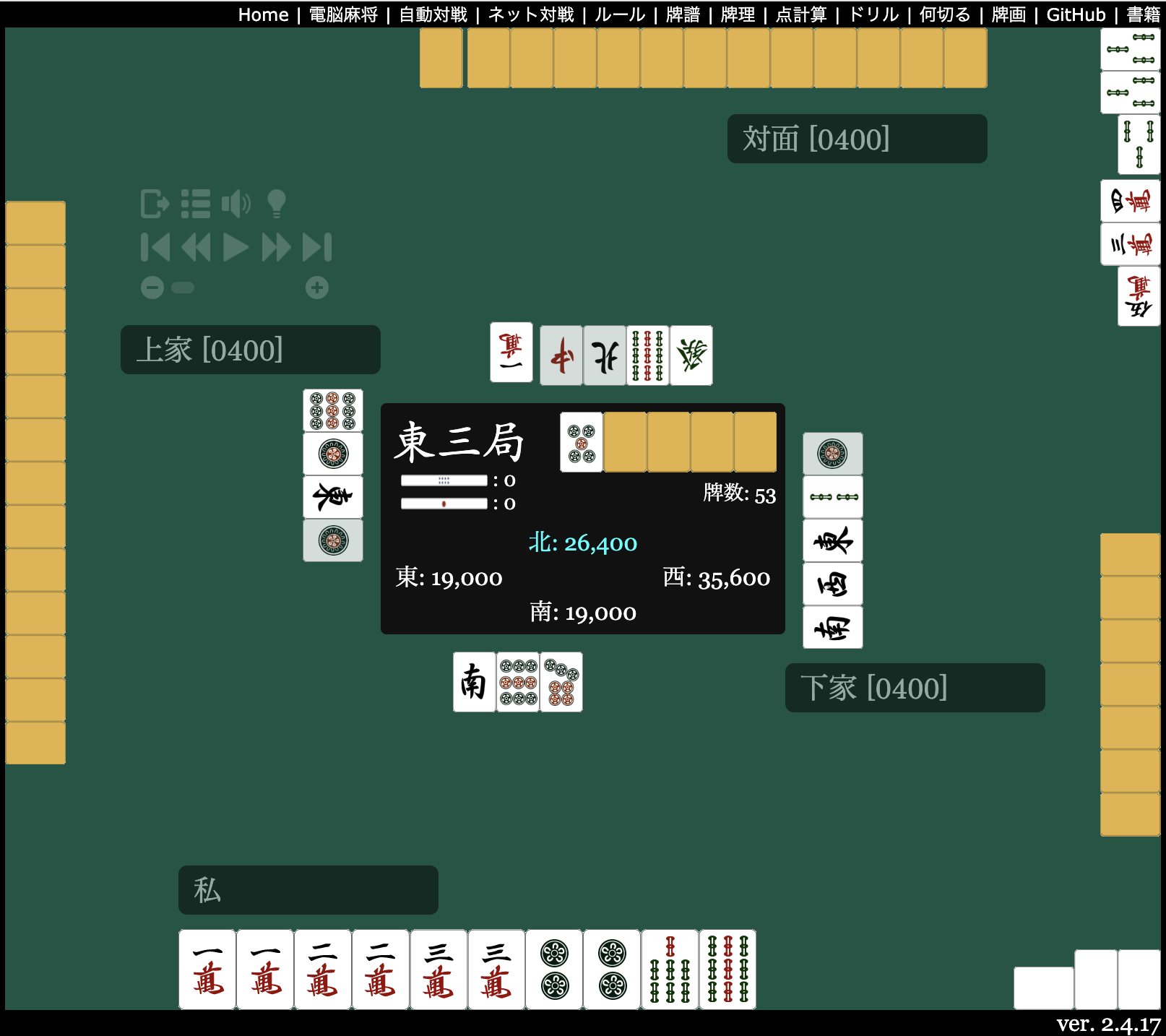
0400 では対面が切った 
をポンする(シャンテン戻ししてのトイトイ狙い)が、これをスルー。
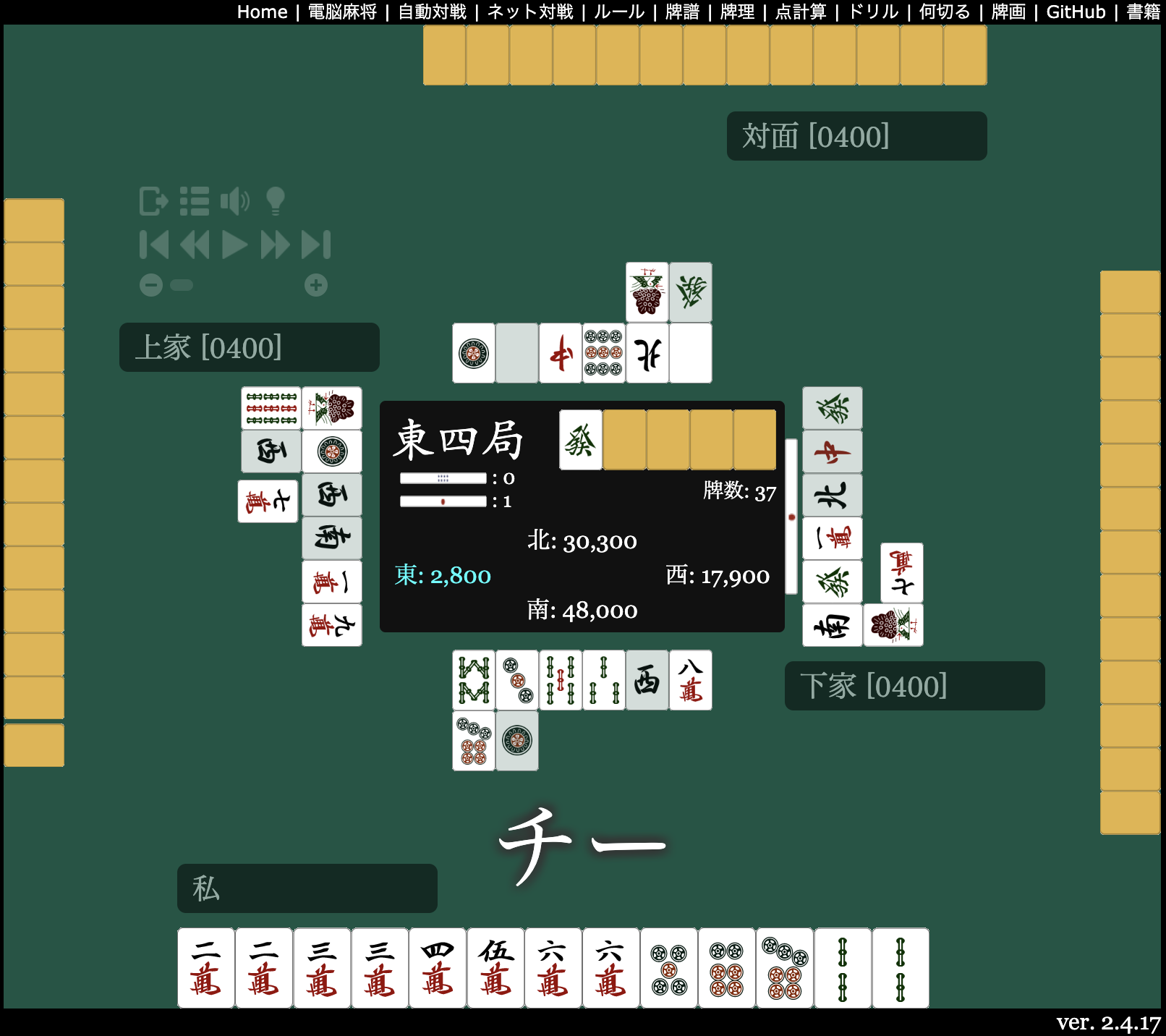
下家のリーチがある状況で 0400 では上家の切った 
をスルーだが、これをチーして 
片アガリのタンヤオのみテンパイにとる。
残り牌数を現在より少なく見積もるため、手を急ぐ傾向が見られます。 具体的には鳴き急ぎやシャンテン戻しを嫌う傾向として現れます。 これを補正するために、異なるシャンテン数を比較するために用いていた係数を以下に変更しました*3。
| シャンテン数 | 0400 | 修正後 |
|---|---|---|
| 0 (聴牌) | 12 | 8 |
| 1 | 12 × 6 | 8 × 4 |
| 2 | 12 × 6 × 3 | 8 × 4 × 2 |
再度デュプリケート対局を行ったところ、平均順位が 2.52 に向上したのでこの値を採用します。
const width = [8, 8*4, 8*4*2];修正後のAIを 0600 として、0400 と10,000戦の デュプリケート対局 を行いました。 (集計後修正する。)
| 0400 | 0600 | 0400 | 0600 | ||
|---|---|---|---|---|---|
| 1位率 | .251 | .253 | 和了率 | .213 | .212 |
| 2位率 | .253 | .252 | 放銃率 | .128 | .128 |
| 3位率 | .248 | .249 | 立直率 | .226 | .227 |
| 4位率 | .254 | .246 | 副露率 | .339 | .334 |
| 平均順位 | 2.49 | 2.49 | 平均打点 | 5,552 | 5,596 |
同一シャンテン数内での選択に変わりはないですが、副露判断とシャンテン戻しに影響があるため、若干の変動があります。 平均順位に変動はほぼありませんが、副露率が若干下がり、平均打点が上昇しました。
| 和了役 | 出現率 | 和了役 | 出現率 | 和了役 | 出現率 | |||
|---|---|---|---|---|---|---|---|---|
| 0400 | 0600 | 0400 | 0600 | 0400 | 0600 | |||
| ドラ | 55.35% | 55.67% | 翻牌 | 39.52% | 39.55% | 対々和 | 0.95% | 1.08% |
| 赤ドラ | 47.59% | 47.68% | 平和 | 14.06% | 14.41% | 三暗刻 | 0.49% | 0.49% |
| 裏ドラ | 20.61% | 20.78% | 断幺九 | 22.44% | 22.60% | 混全帯幺九 | 0.80% | 0.80% |
| 立直 | 47.30% | 47.68% | 一盃口 | 2.67% | 2.73% | 純全帯幺九 | 0.21% | 0.23% |
| ダブル立直 | 0.19% | 0.18% | 三色同順 | 4.06% | 4.08% | 混一色 | 2.16% | 2.24% |
| 一発 | 8.99% | 9.14% | 一気通貫 | 1.96% | 1.82% | 清一色 | 0.19% | 0.20% |
| 門前清自摸和 | 23.72% | 23.83% | 七対子 | 3.26% | 3.10% | 国士無双 | 0.04% | 0.05% |
大きな変動はないですが、一気通貫、七対子の出現率が下がり、その他の役の出現率はやや上昇しました。
次回 からは押し引きの再調整を行います。