はね氏の note 【第2回】麻雀は学習で強くなるか。 によりコンボ理論に注目が集まりました。 コンボ理論 とは、面子を構成できる牌の組合せ数をコンボ数と呼び、安全牌の判断の際にコンボ数が少ない牌をより安全とみなす理論のようです。 このコンボ理論に従って牌の危険度を判断するAIを実装し、実際に対戦させることでその有用性を検証してみました。
宇宙ジン氏の note 【麻雀】コンボ理論について によると、ある牌に対するコンボ数は以下で計算します。
より具体的には、
の総和となります。
具体的な例でコンボ数を計算してみましょう。
以下は はね氏の note にある例です。
上記のダブルリーチの河に対して下記の手牌から何を切るべきか。
はドラとする。
候補を と として、それぞれのコンボ数を求めてみましょう。
は、1枚切れ*1の対子・刻子と 
の両面の可能性があるので、2 + 1 + 4 × 2 = 11 は、1枚切れの対子・刻子と の辺張、
の嵌張の可能性がある*2ので、2 + 1 + 2 × 4 + 4 × 4 = 27となる*3ため、コンボ数の少ない の方が安全という判定になります。
ですが、これは本当に正しいでしょうか？
私にはスジの の方が安全に思えます。
コンボ理論では牌の組合せのみを頼りにするため、愚形と好形が同様の確率で発生するとみなします。 ですが天鳳鳳凰卓の統計では圧倒的に好形待ちが多いことがわかっています。 拙著 対戦型麻雀ゲームAIのアルゴリズムと実装 で紹介している統計では、無スジ1・9牌が両面待ちとなっている確率が 5.23% なのに対し、スジ3・7牌の嵌張・辺張を合わせた確率は 3.01% に過ぎません。
また、コンボ理論のキモは、組合せに使える枚数により待ちの「厚み」を考慮できることと思いますが、安全牌が3枚切られてワンチャンスとなっているときに最後の1枚はリーチ者が持っている可能性が高いことはよく知られており、特に終盤においては厚みを危険度判定に使うことはむしろ誤った結論を導き出す恐れもありそうです。
例題はダブルリーチなので通常より愚形が多く、かつ序盤であるという主張もあると思いますが、いつ使うべきかが明確でない理論は「たまたま上手く行った例」ばかりが強調され、その有用性が判定できないのではないでしょうか。 少なくともプログラム化は困難です。
とは言え、このままではシミュレーションもできないので、今回は「牌の危険度をコンボ数だけで決定する」という実装にして検証します*4。
ここで電脳麻将の危険度計算方法も紹介しておきましょう。 AI同士の対戦を行うときの相手となるアルゴリズムであり、今回の検証はこのアルゴリズムに対してより有用かという検証になるからです。
電脳麻将では以下の表に基づき危険度を決定しています。
| 単騎 | 双碰 | 嵌張 | 辺張 | 両面 | 合計 | |
|---|---|---|---|---|---|---|
| 字牌 | 1 | 2 | 3 | |||
| 1・9牌 | 1 | 2 | 10 | 13 | ||
| 2・8牌 | 1 | 2 | 3 | 10 | 16 | |
| 3・7牌 | 1 | 2 | 3 | 3 | 10 | 19 |
| 4・5・6牌 | 1 | 2 | 3 | 20 | 26 |
先程の例題では、
は、全てのパターンがあり得るので 13点 は、両面が否定されたのでので 9点となり、 の方が安全と判断します。
コンボ理論に従うAIを実装します。
牌の枚数カウントや危険度判定などを行なっているクラス SuanPaiにコンボ数を求めるメソッド calc_combo() を実装しました。
/* 牌 p の手番 l に対するコンボ数を返す */
calc_combo(p, l, c) { // 牌 p が自身の手牌にある場合 c を true とする
let s = p[0], n = +p[1]||5;
let r = 0; // 初期値は 0
if (this._dapai[l][s+n]) return r; // 現物は 0点
const paishu = this._paishu[s];
/* 対子 */
r += Math.max(paishu[n] - (c ? 0 : 1), 0);
// 生牌: 3、1枚切れ: 2、2枚切れ: 1、3枚切れ: 0
/* 刻子 */
r += paishu[n] - (c ? 0 : 1) >= 3 ? 3 // 生牌: 3
: paishu[n] - (c ? 0 : 1) == 2 ? 1 // 1枚切れ: 1
: 0 // 2枚切れ: 0
if (s == 'z') return r; // 字牌の場合は順子の計算は不要
r += n - 2 < 1 ? 0 // 範囲外
: n - 3 >= 1 && this._dapai[l][s+(n-3)] ? 0 // スジ
: paishu[n-2] * paishu[n-1];
r += n - 1 < 1 ? 0 // 範囲外
: n + 1 > 9 ? 0 // 範囲外
: paishu[n-1] * paishu[n+1];
r += n + 2 > 9 ? 0 // 範囲外
: n + 3 <= 9 && this._dapai[l][s+(n+3)] ? 0 // スジ
: paishu[n+1] * paishu[n+2];
return r;
}これを従来の危険度計算メソッド suan_weixian() と交換します。 具体的な牌の危険度は、
とします。 従来のアルゴリズムと同様に危険度の総和は 100 となり、安全牌が増えるごとに(つまり通ったスジが増えるごとに)コンボ数が同じでも危険度が上がっていくことになります。
麻雀AIの作り方 や 鳴かない麻雀の成績への影響をシミュレーションする で説明した方法でAI同士を対戦させます。
元々のAI同士での対戦結果は以下の通りです。
コンボ理論を適用したAIの対戦結果は以下となりました。
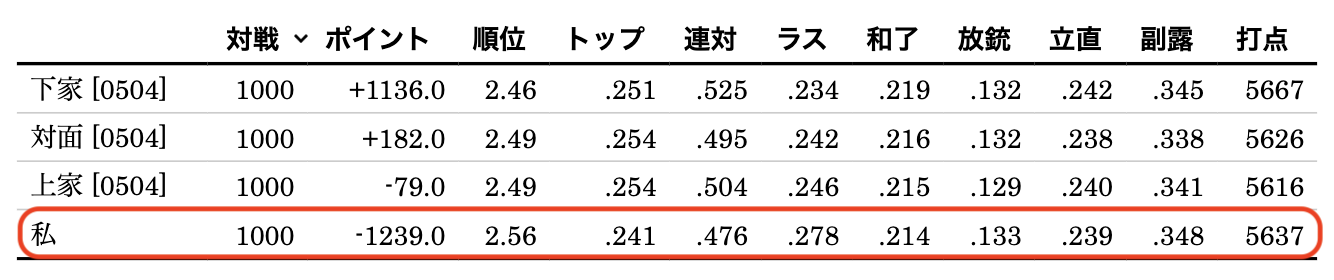
デュプリケート対局 において平均順位が 2.52 → 2.56 と悪化しました。 これは押し引きに関しては相当な改悪と言えます*5。
コンボ理論で具体的にどのような選択を行なったのか、いくつかの事例を見てみましょう。
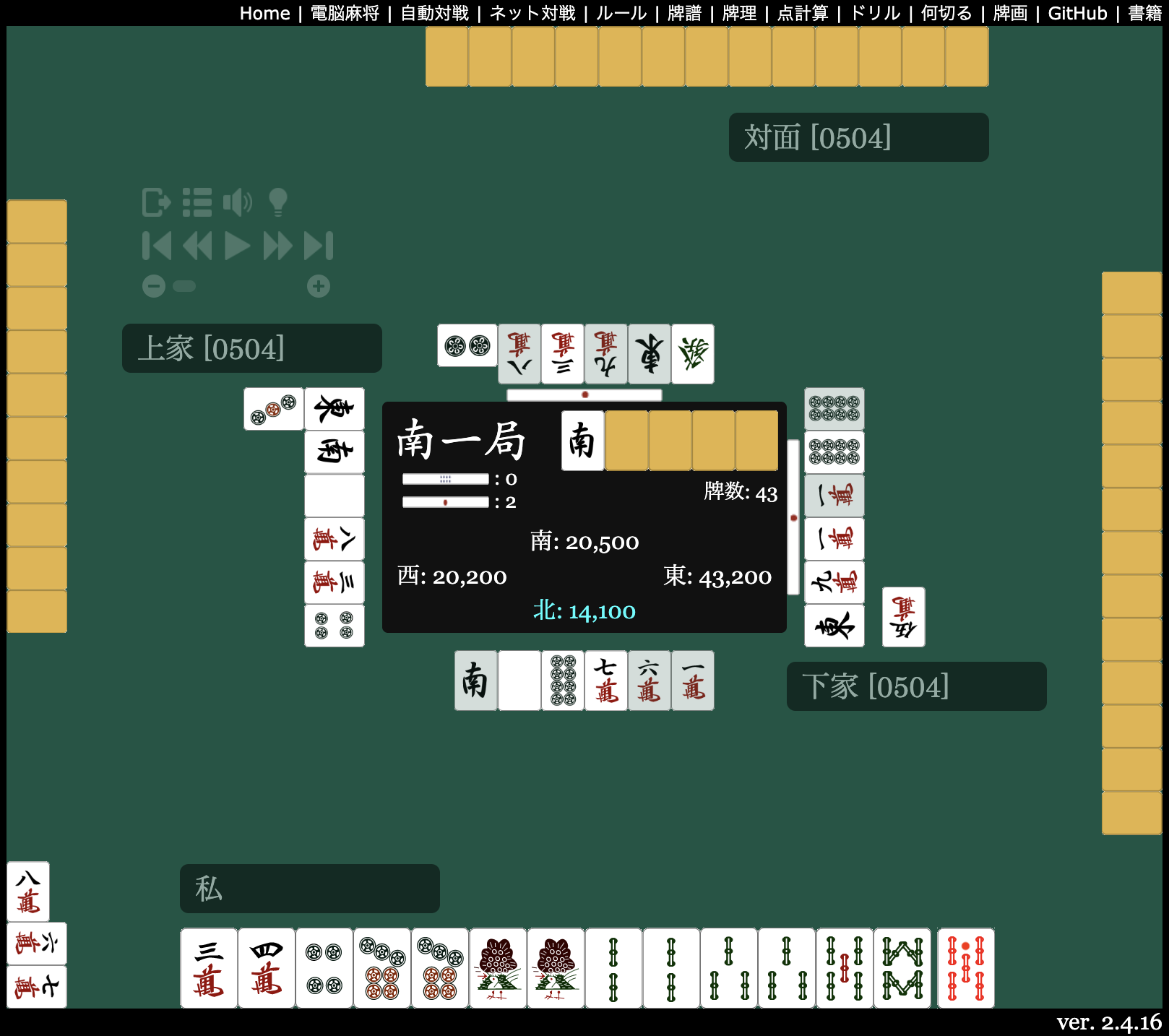
手がかりの少ない状況のため、従来のAIは素直に手を進める 
を選択したが、コンボ理論を適用した場合、 がそれぞれ2枚見えていてコンボ数が最低となる を選択し、七対子に放銃。
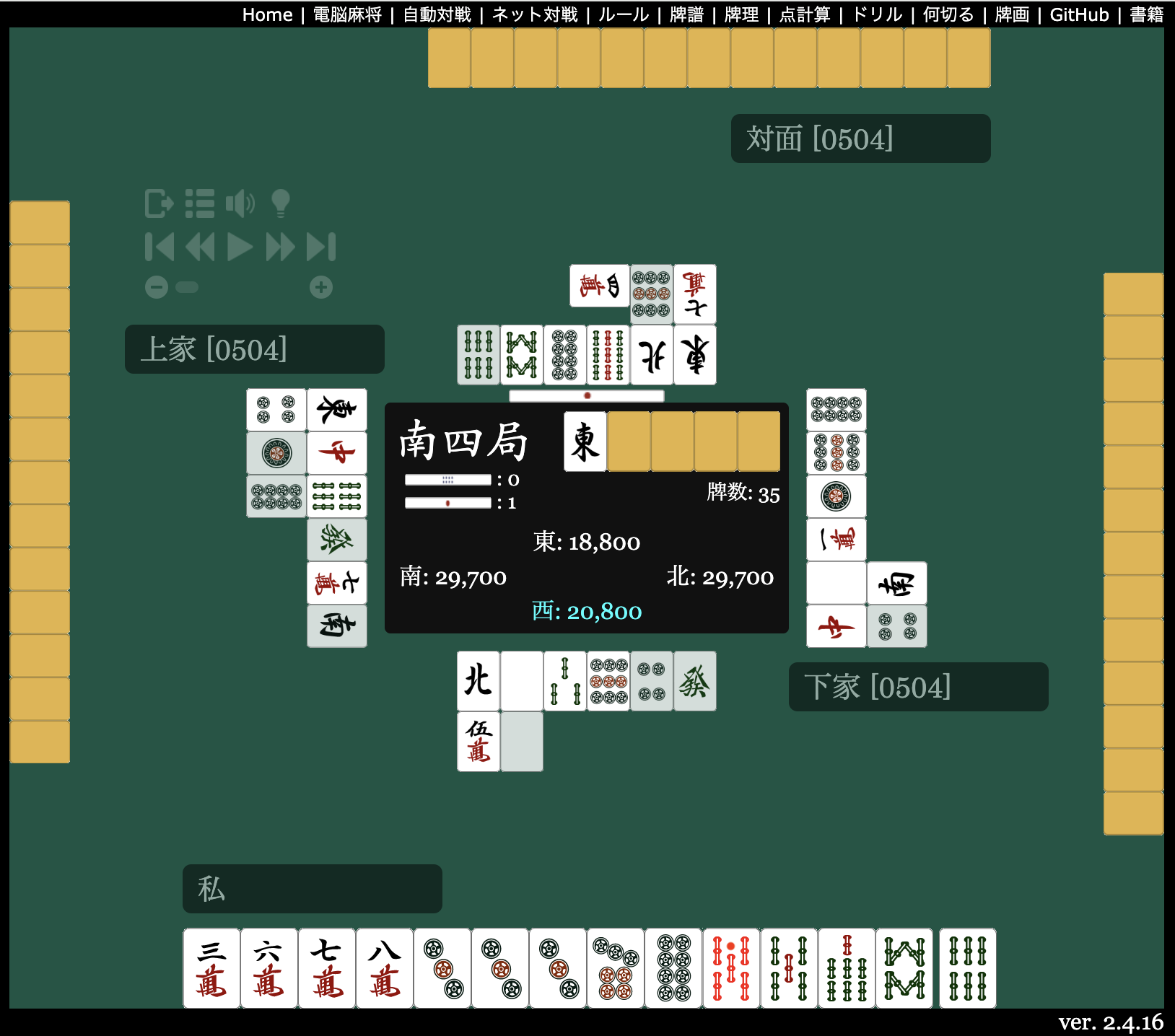
テンパイしたので従来のAIは 切りで追いかけリーチを選択したが、コンボ理論を適用した場合、コンボ数が最大となる を本命の危険牌と判断し、現物の を切ってのオリを選択。
今回のシミュレーションではコンボ理論を全ての局面において単純に適用しましたが、その方法においてコンボ理論は有用な戦術とは言えなさそうです。 具体的にどのような場合に適用すべきか、あるいはどのように「補正」して適用すべきかの指針があればそれに従った実装をして再度検証することも可能ですが、残念ながらネットなどに具体的な指針を見つけることはできませんでした。