Home

牌の危険度決定アルゴリズムを評価する

コンボ理論の有用性を検証する - koba::blog では 電脳麻将 の牌の危険度決定アルゴリズムを単純に コンボ理論 に置き換えて対戦シミュレーションを行いました。 今回は、危険度決定アルゴリズムが実際に当たり牌をどの程度正しく予想できているか、という観点で実際の天鳳の牌譜を使って評価してみます。

実験方法

2024年の天鳳 鳳凰卓 東南戦 184,426 戦における、フリテン・カラテン*1および国士無双のリーチを除く全ての「先制リーチ」*2について、リーチ者の下家目線*3でリーチ宣言直後とその局の最後のツモの直後のタイミングで危険度を計算し、リーチの実際の待ちとの乖離で評価します。 リーチ後の見逃しによるフリテンが発生した場合は、その局の最後のツモでの評価は行いません。

危険度決定アルゴリズム

例題

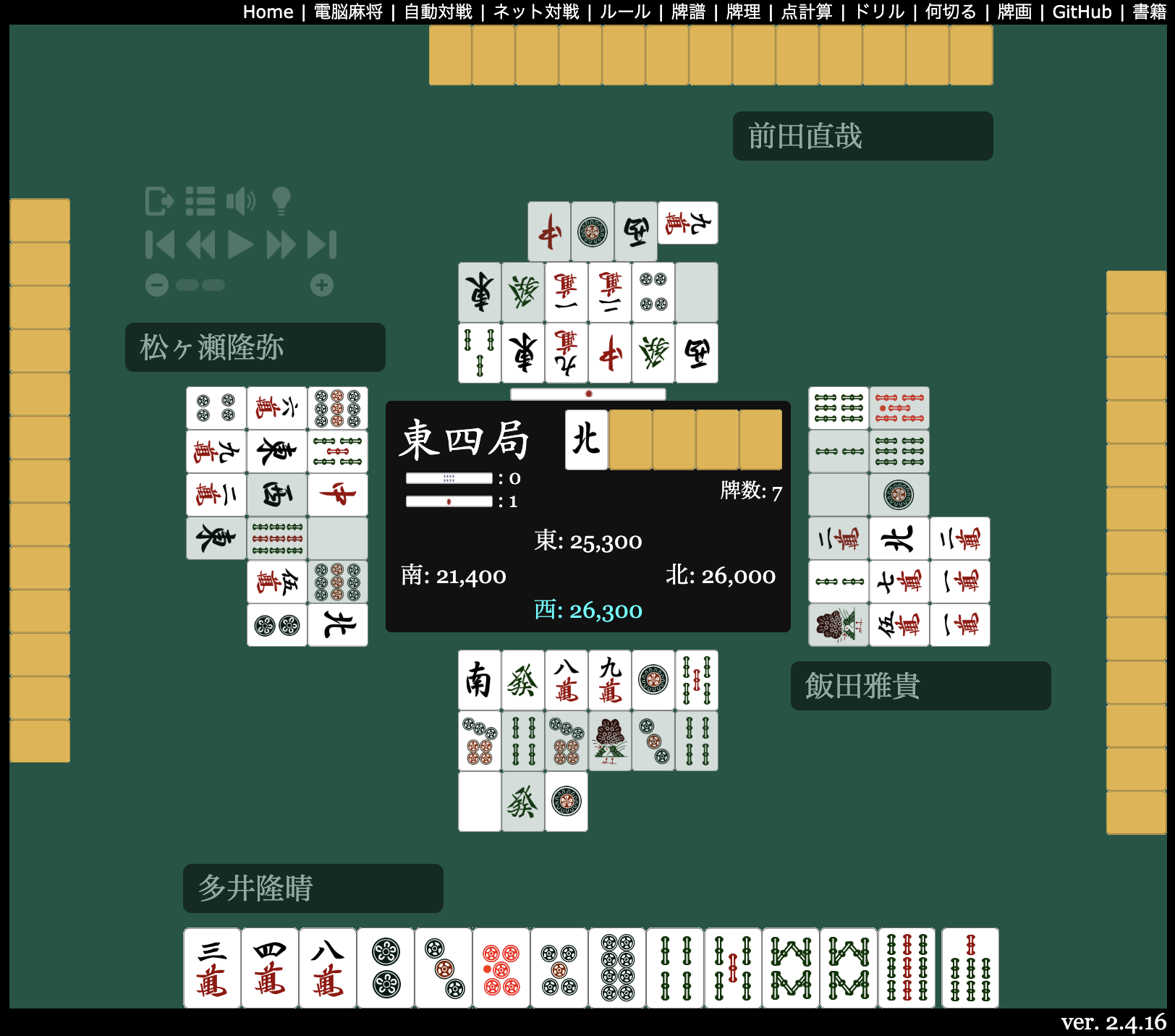
上図の局面*4を例に評価対象とする危険度決定アルゴリズムを説明します。 危険度はその総和を 1 とする確率と見なせるように正規化します*5。

推定なし

現物以外の全ての牌の危険度を同一とします。 上記の例の場合、現物は11種なので、正規化した危険度は 1 / (34 - 11) = 0.043 となります。

1 2 3 4 5 6 7 8 9
m 0.0430.0430.0430.0430.0430.043
p 0.0430.043 0.0430.0430.0430.0430.043
s 0.0430.043 0.0430.0430.0430.0430.0430.043
z 0.043 0.043

考え得る最悪の方法であるので、この方法を評価の基準とします。

コンボ理論

各牌について、捨て牌・自身の手牌・他者の副露面子・ドラ表示牌として見えていない牌を使って対子・刻子・順子を構成できる組合せの数をコンボ数とします。 具体的には、

の総和となります。

上記の例で実際に当たり牌であった s7 のコンボ数は 3 + 3 + (0 × 2) + (2 × 2) + (2 × 2) = 14 となり、コンボ数の総和が 279 なので、正規化した危険度は 14 / 279 = 0.050 となります。

上段をコンボ数、下段を正規化した危険度とすると全ての牌の危険度は以下となります。

1 2 3 4 5 6 7 8 9
m 12
0.043		18
0.065		19
0.068		15
0.054		15
0.054		12
0.043
p 7
0.025		11
0.039		 23
0.082		20
0.072		19
0.068		18
0.065		 7
0.025
s 7
0.025		10
0.036		 7
0.025		11
0.039		 7
0.025		14
0.050		15
0.054		 9
0.032
z 3
0.011		 0
0.000

電脳麻将(旧方式)

電脳麻将で過去に採用していた方式です。 『現代麻雀技術論』の「牌の危険度」 を参考にした以下の 表を元に危険度を決定していました。

牌の種類 無スジ 片スジ スジ 生牌 1枚切れ2枚切れラス牌
字牌 − − − 3 2 1 0
1・9牌 6 − 3 − − − −
2・8牌 8 − 4 − − − −
3・7牌 8 − 5 − − − −
4・5・6牌 12 8 4 − − − −

上記の例で s7 は「無スジ 3・7牌」になるので危険度は 8、正規化すると 8 / 179 = 0.045 となります*6。

1 2 3 4 5 6 7 8 9
m 8
0.045		 8
0.045		 8
0.045		 8
0.045		 8
0.045		 8
0.045
p 8
0.045		 8
0.045		 12
0.068		12
0.068		 5
0.028		 8
0.045		 6
0.034
s 6
0.034		 8
0.045		 12
0.068		12
0.068		 8
0.045		 8
0.045		 8
0.045		 6
0.034
z 2
0.011		 0
0.000

電脳麻将(現方式)

電脳麻将の現在のアルゴリズムです。 以下の 表 に基づき、危険度を決定します。

単騎 双碰 嵌張 辺張 両面 合計
字牌 1 2 3
1・9牌 1 2 10 13
2・8牌 1 2 3 10 16
3・7牌 1 2 3 3 10 19
4・5・6牌 1 2 3 20 26

上記の例で s7 は s5 のカベにより両面が否定されるので危険度は 9、正規化すると 9 / 314 = 0.029 となります*7。

1 2 3 4 5 6 7 8 9
m 13
0.041		16
0.051		14
0.045		16
0.051		16
0.051		13
0.041
p 13
0.041		16
0.051		 26
0.083		26
0.083		 7
0.022		16
0.051		11
0.035
s 11
0.035		14
0.045		 11
0.035		23
0.073		11
0.035		 9
0.029		16
0.051		13
0.041
z 3
0.010		 0
0.000

電脳麻将(改良案)

電脳麻将の現在のアルゴリズムをコンボ理論を使って改良してみます。 電脳麻将の現在のアルゴリズムでは待ちの形をカベのみで否定していますが、ここにコンボ理論を適用しコンボ数を待ちの「厚さ」とします。

上記の例で s7 は 1 × (3 / 3) + 2 × (3 / 3) + 3 × (2 × 2 / 16) + 3 × (2 × 2 / 16) + 10 × (0 × 2 / 16) = 4.50、正規化すると 4.50 / 125.65 = 0.036 となります。

1 2 3 4 5 6 7 8 9
m 6.75
0.054		 7.88
0.063		 7.65
0.061		 6.21
0.049		 6.21
0.049		 6.96
0.055
p 3.83
0.031		 4.58
0.036		 10.33
0.082		10.00
0.080		 3.71
0.030		 8.75
0.070		 4.08
0.032
s 4.08
0.032		 3.33
0.027		 4.08
0.032		 6.00
0.048		 4.08
0.032		 4.50
0.036		 6.21
0.049		 5.08
0.040
z 1.33
0.011		 0.00
0.000

評価方法

天鳳 鳳凰卓 東南戦の1年分の牌譜を例に牌の危険度を計算し、実際の待ちとの乖離を 二乗平均平方根誤差 と 交差エントロピー誤差 で評価します。

二乗平均平方根誤差

ある牌の予測危険度を pi 、実際の危険度を yi とすると、二乗平均平方根誤差 は

で求めることができます。 ある牌が実際に待ちである場合は yi は 1、待ちでない場合は 0 としますが、両面待ちなど複数の牌が待ちになっている場合はその総和が 1 となるよう正規化します。 例えば p3 p6 が待ちとなっているときは、そのそれぞれの危険度を 0.5 とします。

最初の例の局面における危険度をコンボ理論で計算した場合、その二乗平均平方根誤差は 0.16739、電脳麻将(現方式)では 0.17102 になります。 値が 0 に近いほど予測は正しいと評価できます。

交差エントロピー誤差

ある牌の予測危険度を pi 、実際の危険度を yi とすると、交差エントロピー誤差 は

で求めることができます。 交差エントロピーでは実際の危険度は 0 か 1 のどちらかであり正規化はしません。 そのため上記式は、その牌が待ちであるときは log( pi )、待ちでないときは log( 1 − pi ) とした総和になります*8。 複数の牌が待ちになっている場合は、そのそれぞれについて交差エントロピーを求め、その平均を解とします。

最初の例の局面における危険度をコンボ理論で計算した場合、その交差エントロピー誤差は 3.96832、電脳麻将(現方式)では 4.55003 になります。

評価結果

2024年の天鳳 鳳凰卓 東南戦 1年分の牌譜データを用いて牌の危険度を計算し、それを二乗平均平方根誤差と交差エントロピー誤差で評価しました。 評価には以下のプログラムを使用しました。

評価結果は以下のとおりです。

二乗平均平方根誤差 交差エントロピー誤差
立直直後 終局直前 立直直後 終局直前
推定なし 0.12929 0.12717 4.24517 3.87907
コンボ理論 0.12840 0.12613 4.12743 3.79744
電脳麻将(旧方式) 0.12839 0.12587 4.12966 3.78530
電脳麻将(現方式) 0.12830 0.12545 4.12207 3.76095
電脳麻将(改良案) 0.12818 0.12560 4.11313 3.77279

この結果を見る限り コンボ理論はそのままでは適用できない と思われます*9。 電脳麻将の現方式とコンボ理論を組み合わせた電脳麻将の改良案は有望そうですが、局終盤で精度が悪くなる点が気になります*10。

ダマテンの効果をシミュレーションする
コンボ理論の有用性を検証する
TOP
  1. ^ 正確には単騎待ちしかありえない牌(多くの場合は字牌)が3枚切れのケース
  2. ^ その局での最初のリーチの意味
  3. ^ ドラ表示牌、4者の捨て牌と副露牌、下家自身の手牌が把握できる状態
  4. ^ Mトーナメント・多井プロの７ｓ放銃を振り返る｜t-yoko@MリーグをNAGAで解析 より
  5. ^ 実際には両面待ちなど複数の牌で和了できることが多く総和は 1 にはなりませんが、当たり牌数は予測できないため 1 に正規化します
  6. ^ ただしこの表は優先順位を示しており、正規化は考慮していませんでした
  7. ^ つまり電脳麻将(現方式)では、多井選手の手牌で一番安全に見える牌は s7 になる訳です
  8. ^ log(0) は無限大になるため、待ちとなっている牌を危険度 0 と予測したり、待ちでない牌を危険度 1 とした場合には誤差が無限大となり測定の意味をなしません。フリテンやカラテンのケースを除外しないとこの問題が発生します
  9. ^ ネットにあるコンボ理論で危険牌を当てる事例はたまたま上手く行った例と考えるのがよさそうです
  10. ^ 局終盤のワンチャンスは信頼できないとはよく聞きます